API usage and design overview

In ths document we give an overview on the structure of the interfaces, classes and packages of JAS. In the first section we show how to compute Legendre polynomials with the JAS API. In the next three sections we focus on the structure of the required types and the creation of the corresponding objects. In the following three sections we focus on the functional aspects of the types, i.e. their constructors and methods. For a discussion of other design alternatives see the problems document. Further programming issues and bugs are listed in the Findbugs report.

1. Getting started

You can use whatever environment for programming in Java you like. The next picture shows the usage of Eclipse, but any text editor and a Java compiler will do as well.

 
JAS program to compute Legendre polynomials in the Eclipse IDE

1.1. Computation of the Legendre polynomials

• P[0](x) = 1
• P[1](x) = x
• P[n](x) = 1/n ( (2n-1) x P[n-1] - (n-1) P[n-2] ).

P[0] = 1 
P[1] = x
P[2] = 3/2 x^2 - 1/2 
P[3] = 5/2 x^3 - 3/2 x
P[4] = 35/8 x^4 - 15/4 x^2 + 3/8 
P[5] = 63/8 x^5 - 35/4 x^3 + 15/8 x
P[6] = 231/16 x^6 - 315/16 x^4 + 105/16 x^2 - 5/16 
P[7] = 429/16 x^7 - 693/16 x^5 + 315/16 x^3 - 35/16 x
P[8] = 6435/128 x^8 - 3003/32 x^6 + 3465/64 x^4 - 315/32 x^2 + 35/128 
P[9] = 12155/128 x^9 - 6435/32 x^7 + 9009/64 x^5 - 1155/32 x^3 + 315/128 x

The polynomials have been computed with the following Java program. First we need a polynomial ring ring over the rational numbers, in one variable "x" and a list P to store the computed polynomials. The polynomial factory object itself needs at least a factory for the creation of coefficients and the number of variables. Additionally the term order and names for the variables can be specified. With this information the polynomial ring factory can be created by new GenPolynomialRing <BigRational>(fac,1,var), where fac is the coefficient factory, 1 is the number of variables, and var is an String array of names.

    BigRational fac = new BigRational();
    String[] var = new String[]{ "x" };
    GenPolynomialRing<BigRational> ring
        = new GenPolynomialRing<BigRational>(fac,1,var);

    int n = 10;
    List<GenPolynomial<BigRational>> P 
       = new ArrayList<GenPolynomial<BigRational>>(n);
    GenPolynomial<BigRational> t, one, x, xc;
    BigRational n21, nn;

    one = ring.getONE();
    x   = ring.univariate(0);

    P.add( one );
    P.add( x );
    for ( int i = 2; i < n; i++ ) {
        n21 = new BigRational( 2*i-1 );
        xc = x.multiply( n21 );
        t = xc.multiply( P.get(i-1) );  // (2n-1) x P[n-1]
        nn = new BigRational( i-1 );
        xc = P.get(i-2).multiply( nn ); // (n-1) P[n-2]
        t = t.subtract( xc );
        nn = new BigRational(1,i);      
        t = t.multiply( nn );           // 1/n t
        P.add( t );
    }
    for ( int i = 0; i < n; i++ ) {
        System.out.println("P["+i+"] = " + P.get(i).toString(var) );
        System.out.println();
    }

The polynomials for the recursion base are one and x. Both are generated from the polynomial ring factory with method ring.getONE() and ring.univariate(0), respectively. The polynomial (2n-1)x is produced in the for-loop by n21 = new BigRational( 2*i-1 ); and xc = x.multiply( n21 );. The polynomial (n-1) P[n-2] is computed by nn = new BigRational( i-1 ); and xc = P.get(i-2).multiply( nn ). Finally we have to multiply the difference of the intermediate polynomials by 1/i as nn = new BigRational( 1, i ); and t = t.multiply( nn ). Then, in the for-loop, the polynomials P[i] are computed using the definition, and stored in the list P for further use. In the last for-loop, the polynomials are printed, producing the output shown above. The string representation of the polynomial object can be created, as expected, by toString(), or by using names for the variables with toString(var). The imports required are

import java.util.ArrayList;
import java.util.List;
import edu.jas.arith.BigRational;
import edu.jas.poly.GenPolynomial;
import edu.jas.poly.GenPolynomialRing;

To use other coefficient rings, one simply changes the generic type parameter, say, from BigRational to BigComplex and adjusts the coefficient factory. The factory would then be created as c = new BigComplex(), followed by new GenPolynomialRing<BigComplex> (c,1,var). This small example shows that this library can easily be used, just as any other Java package or library.

In the following sections we describe the central classes and interfaces for the polynomial API.

1.2. Algebraic structures overview

To get an idea of the scope of JAS we summarize the implemented algebraic structures and of the implemented algebraic algorithms.

"Arithmetic" means implementation of the methods defined in the interface RingElem. As of 2021-03 there are 36 rings implemented (9 explicit, others generic). To be continued.

1.3. Algebraic algorithms overview

The following table contains an overview of implemented algebraic algorithms.

1.4. Packages and components overview

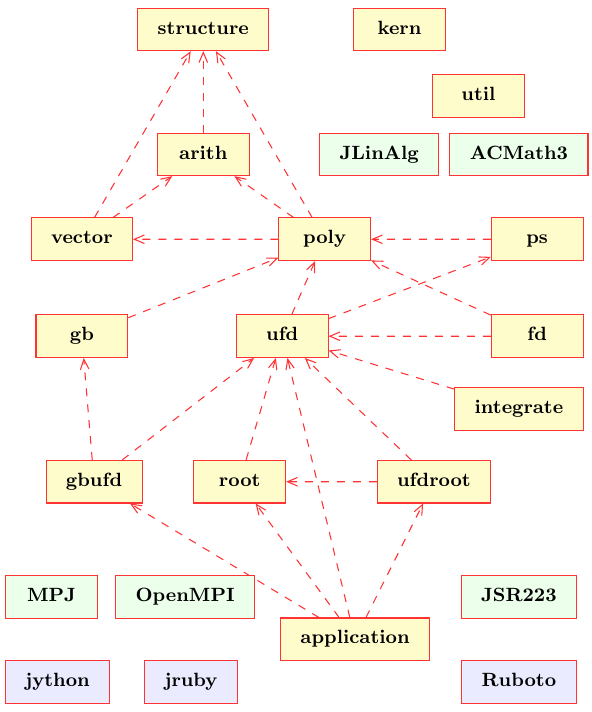
More details can be found in the JDepend report.txt.

2. Recursive ring element design

The next figure gives an overview of the central interfaces and classes. The interface RingElem defines a recursive type which defines the functionality (see next section) of the polynomial coefficients and is also implemented by the polynomials itself. So polynomials can be taken as coefficients for other polynomials, thus defining a recursive polynomial ring structure.

Since the construction of constant ring elements has been difficult in previuos designs, we separated the creational aspects of ring elements into ring factories with sufficient context information. The minimal factory functionality is defined by the interface RingFactory. Constructors for polynomial rings will then require factories for the coefficients so that the construction of polynomials over these coefficient rings poses no problem. The ring factories are additionaly required because of the Java generic type design. I.e. if C is a generic type name it is not possible to construct an new object with new C(). Even if this would be possible, one can not specify constructor signatures in Java interfaces, e.g. to construct a one or zero constant ring element. Recursion is again achieved by using polynomial factories as coefficient factories in recursive polynomial rings. Constructors for polynomials will always require a polynomial factory parameter which knows all details about the polynomial ring under consideration.

UML diagram of JAS types

3. Coefficients and polynomials

We continue the discussion of the next layer of classes in the the above figure.

Elementary coefficient classes, such as BigRational or BigInteger, implement both the RingElem and RingFactory interfaces. This is convenient, since these factories do not need further context information. In the implementation of the interfaces the type parameter C extends RingElem<C> is simultaneously bound to the respective class, e.g. BigRational. Coefficient objects can in most cases created directly via the respective class constructors, but also via the factory methods. E.g. the object representing the rational number 2 can be created by new BigRational(2) or by fac = new BigRational(), fac.fromInteger(2) and the object representing the rational number 1/2 can be created by new BigRational(1,2) or by fac.parse("1/2").

Generic polynomials are implemented in the GenPolynomial class, which has a type parameter C extends RingElem<C> for the coefficient type. So all operations on coefficients required in polynomial arithmetic and manipulation are guaranteed to exist by the RingElem interface. The constructors of the polynomials always require a matching polynomial factory. The generic polynomial factory is implemented in the class GenPolynomialRing, again with type parameter C extends RingElem<C> (not RingFactory). The polynomial factory however implements the interface RingFactory<C extends RingElem<C>> so that it can also be used recursively. The constructors for GenPolynomialRing require at least parameters for a coefficient factory and the number of variables of the polynomial ring.

Having generic polynomial and elementary coefficient implementations one can attempt to construct polynomial objects. The type is first created by binding the type parameter C extends RingElem<C> to the desired coefficient type, e.g. BigRational. So we arrive at the type GenPolynomial<BigRational>. Polynomial objects are then created via the respective polynomial factory of type GenPolynomialRing<BigRational>, which is created by binding the generic coefficient type of the generic polynomial factory to the desired coefficient type, e.g. BigRational. A polynomial factory object is created from a coefficient factory object and the number of variables in the polynomial ring as usual with the new operator via one of its constructors. Given an object coFac of type BigRational, e.g. created with new BigRational(), a polynomial factory object pfac of the above described type could be created by new GenPolynomialRing<BigRational>(coFac,5). I.e. we specified a polynomial ring with 5 variables over the rational numbers. A polynomial object p of the above described type can then be created by any method defined in RingFactory, e.g. by pfac.getONE(), pfac.fromInteger(1), pfac.random(3) or pfac.parse("(1)").

Since GenPolynomial itself implements the RingElem interface, they can also be used recursively as coefficients. We continue the polynomial example and are going to use polynomials over the rational numbers as coefficients of a new polynomial. The type is then GenPolynomial<GenPolynomial<BigRational>> and the polynomial factory has type GenPolynomialRing<GenPolynomial<BigRational>>. Using the polynomial coefficient factory pfac from above a recursive polynomial factory rfac could be created by new GenPolynomialRing<GenPolynomial<BigRational>>(pfac,3). The creation of a recursive polynomial object r of the above described type is then as a easy as before e.g. by rfac.getONE(), rfac.fromInteger(1) or rfac.random(3).

4. Solvable polynomials

We turn now to the last layer of classes in the the above figure.

The generic polynomials are intended as super class for further types of polynomial rings. As one example we take so called solvable polynomials, which are like normal polynomials but are equipped with a new non-commutative multiplication. They are implemented in the class GenSolvablePolynomial which extends GenPolynomial and inherits all methods except clone() and multiply(). The class also has a type parameter C extends RingElem<C> for the coefficient type. Note, that the inherited methods are in fact creating solvable polynomials since they employ the solvable polynomial factory for the creation of any new polynomial internally. Only the formal method return type is that of GenPolynomial, the run-time type is GenSolvablePolynomial to which they can be casted at any time. The factory for solvable polynomials is implemented by the class GenSolvablePolynomialRing which also extends the generic polynomial factory. So this factory can also be used in the constructors of GenPolynomial via super() to produce in fact solvable polynomials internally. The data structure is enhanced by a table of non-commutative relations defining the new multiplication. The constructors delegate most things to the corresponding super class constructors and additionally have a parameter for the RelationTable to be used. Also the methods delegate the work to the respective super class methods where possible and then handle the non-commutative multiplication relations separately.

The construction of solvable polynomial objects follows directly that of polynomial objects. The type is created by binding the type parameter C extends RingElem<C> to the desired coefficient type, e.g. BigRational. So we have the type GenSolvablePolynomial<BigRational>. Solvable polynomial objects are then created via the respective solvable polynomial factory of type GenSolvablePolynomialRing<BigRational>, which is created by binding the generic coefficient type of the generic polynomial factory to the desired coefficient type, e.g. BigRational. A solvable polynomial factory object is created from a coefficient factory object, the number of variables in the polynomial ring and a table containing the defining non-commutative relations as usual with the new operator via one of its constructors. Given an object coFac of type BigRational as before, a polynomial factory object spfac of the above described type could be created by new GenSolvablePolynomialRing<BigRational>(coFac,5). I.e. we specified a polynomial ring with 5 variables over the rational numbers with no commutator relations. A solvable polynomial object p of the above described type can then be created by any method defined in RingFactory, e.g. by spfac.getONE(), spfac.fromInteger(1), spfac.random(3) or spfac.parse("(1)"). Some care is needed to create RelationTable objects since its constructor requires the solvable polynomial ring which is under construction as parameter. It is most convenient to first create a GenSolvablePolynomialRing with an empty relation table and then to add the defining relations.

5. Ring element and factory functionality

The following sections and the next figure gives an overview of the functionality of the main interfaces and polynomial classes.

The RingElem interface has a generic type parameter C which is constrained to a type with the same functionality C extends RingElem<C>. It defines the usual methods required for ring arithmetic such as C sum(C S); C subtract(C S); C negate(); C abs(); C multiply(C S); C divide(C S); C remainder(C S); C inverse(); Although the actual ring may not have inverses for every element or some division algorithm we have included these methods in the definition. In a case where there is no such function, the implementation may deliberately throw a RuntimeException or choose some other meaningful element to return. The method isUnit() can be used to check if an element is invertible.

Besides the arithmetic method there are following testing methods boolean isZERO(); boolean isONE(); boolean isUnit(); int signum(); boolean equals(Object b); int hashCode(); int compareTo(C b); The first three test if the element is 0, 1 or a unit in the respective ring. The signum() method defines the sign of the element (in case of an ordered ring). equals(), hashCode() and compareTo() are required to keep Javas object machinery working in our sense. They are used when an element is put into a Java collection class, e.g. Set, Map or SortedMap. The last method C clone() can be used to obtain a copy of the actual element. As creational method one should better use the method C copy(C a) from the ring factory, but in Java it is more convenient to use the clone() method.

As mentioned before, the creational aspects of rings are separated into a ring factory. A ring factory is intended to store all context information known or required for a specific ring. Every ring element should also know its ring factory, so all constructors of ring element implementations require a parameter for the corresponding ring factory. Unfortunately constructors and their signature can not be specified in a Java interface. The RingFactory interface also has a generic type parameter C which is constrained to a type with the ring element functionality C extends RingElem<C>. The defined methods are C getZERO(); C getONE(); C fromInteger(long a); C fromInteger(java.math.BigInteger a); C random(int n); C copy(C c); C parse(String s); C parse(Reader r); The first two create 0 and 1 of the ring. The second two are used to embed a natural number into the ring and create the corresponding ring element. The copy() method was intended as the main means to obtain a copy of a ring element, but it is now no more used in our implmentation. Instead the clone() method is used from the ring element interface. The random(int n) method creates a random element of the respective ring. The parameter n specifies an appropriate maximal size for the created element. In case of coefficients it usually means the maximal bit-length of the element, in case of polynomials it influences the coefficient size and the degrees. For polynomials there are random() methods with more parameters. The two methods C parse(String s) and C parse(Reader r) create a ring element from some external string representation. For coefficients this is mostly implemented directly and for polynomials the class GenPolynomialTokenizer is employed internally. In the current implementation the external representation of coefficients may never contain white space and must always start with a digit. In the future the ring factory will be enhanced by methods that test if the ring is commutative, associative or has some other important property or the value of a property, e.g. is an euclidean ring, is a field, an integal domain, a uniqe factorization domain, its characteristic or if it is noetherian.

UML diagram of JAS type functionality

6. Polynomial and polynomial factory functionality

We continue the discussion of the above figure with the generic polynomial and factory classes.

The GenPolynomial class has a generic type parameter C which is constrained to a type with the functionality of ring elements C extends RingElem<C>. Further the class implements a RingElem over itself RingElem<GenPolynomial<C>> so that it can be used for the coefficients of an other polynomial ring. The functionality of the ring element methods has already been explained in the previous section. There are two public and one protected constructors, each requires at least a ring factory parameter GenPolynomialRing<C> r. The first creates a zero polynomial GenPolynomial(. r), the second creates a polynomial of one monomial with given coefficient and exponent tuple GenPolynomial(. r, C c, ExpVector e), the third creates a polynomial from the internal sorted map of an other polynomial GenPolynomial(. r, SortedMap<ExpVector,C> v). Further there are methods to access parts of the polynomial like leading term, leading coefficient (still called leading base coefficient from the Aldes/SAC-2 tradition) and leading monomial. The toString() method creates as usual a string representation of the polynomials consisting of exponent tuples and coefficients. One variant of it takes an array of variable names and creates a string consisting of coefficients and products of powers of variables. The method extend() is used to embed the polynomial into the 'bigger' polynomial ring specified in the first parameter. The embeded polynomial can also be multiplied by a power of a variable. The contract() method returns a map of exponents and coefficients. The coefficients are polynomials belonging to the 'smaller' polynomial ring specified in the first parameter. If the polynomial actually belongs to the smaller polynomial ring the map will contain only one pair, mapping the zero exponent vector to the polynomial with variables removed. A last group of methods computes (extended) greatest common divisors. They work correct for univariate polynomials over a field but not for arbitrary multivatiate polynomials. These methods will be moved to a new separate class in the future.

The GenPolynomialRing class has a generic type parameter C which is constrained to a type with the functionality of ring elements C extends RingElem<C>. Further the class implements a RingFactory over GenPolynomial<C> so that it can be used as coefficient factory of a different polynomial ring. The constructors require at least a factory for the coefficents as first parameter of type RingFactory<C> and the number of variables in the second parameter. A third parameter can optionally specify a TermOrder and a fourth parameter can specify the names for the variables of the polynomial ring. Besides the methods required by the RingFactory interface there are additional random() methods which provide more control over the creation of random polynomials. They have the following parameters: the bitsize of random coefficients to be used in the random() method of the coefficient factory, the number of terms (i.e. the length of the polynomial), the maximal degree in each variable and the density of nozero exponents, i.e. the ratio of nonzero to zero exponents. The toString() method creates a string representation of the polynomial ring consisting of the coefficient factory string representation, the tuple of variable names and the string representation of the term order. The extend() and contract() methods create 'bigger' respectively 'smaller' polynomial rings. Both methods take a parameter of how many variables are to be added or removed form the actual polynomial ring. extend() will setup an elimination term order consisting of two times the actual term order when ever possible.

7. Solvable polynomial and solvable polynomial factory functionality

We continue the discussion of the above figure with the generic solvable polynomial and factory classes.

The GenSolvablePolynomial class has a generic type parameter C which is constrained to a type with the functionality of ring elements C extends RingElem<C>. The class extends the GenPolynomial class. It inherits all additive functionality and overwrites the multiplicative functionality with a new non-commutative multiplication method. Unfortunately it cannot implement a RingElem over itself RingElem<GenSolvablePolynomial<C>> but can only inherit the implementation of RingElem<GenPolynomial<C>> from its super class. By this limitation a solvable polynomial can still be used as coefficent in another polynomial, but only with the type of its super class. The limitation comes form the erasure of template parameters in RingElem<...> to RingElem for the code generated. I.e. the generic interfaces become the same after type erasure and it is not allowed to implement the same interface twice. There are two public and one protected constructors as in the super class. Each requires at least a ring factory parameter GenSolvablePolynomialRing<C> r which is stored in a variable of this type shadowing the variable with the same name of the super factory type. The rest of the initialization work is delegated to the super class constructor.

The GenSolvablePolynomialRing class has a generic type parameter C which is constrained to a type with the functionality of ring elements C extends RingElem<C>. The class extends the GenPolynomialRing class. It overwrites most methods to implement the new non-commutative methods. Also this class cannot implement a RingFactory over GenSolvablePolynomial<C>. It only implements RingFactory over GenPolynomial<C> by inheritance by the same reason of type erasure as above. But it can be used as coefficient factory with the type of its super class for a different polynomial ring. One part of the constructors just restate the super class constructors with the actual solvable type. A solvable polynomial ring however must know how to perform the non-commutative multiplication. To this end a data structure with the respective commutator relations is required. It is implemented in the RelationTable class. The other part of the constructors additionaly takes a parameter of type RelationTable to set the initial commutator relation table. Some care is needed to create relation tables and solvable polynomial factories since the relation table requires a solvable polynomial factory as parameter in the constructor. So it is most advisable to create a solvable polynomial factory object with empty relation table and to fill it with commutator relations after the constructor is completed but before the factory will be used. There is also a new method isAssociative() which tries to check if the commutator relations indeed define an associative algebra. This method should be extracted to the RingFactory interface together with a method isCommutative(), since both are of general importance and not always fulfilled in our rings. E.g. BigQuaternion is not commutative and so is a polynomial ring over these coefficents is not commutative. The same applies to associativity and the (not jet existing) class BigOctonion.

This concludes the discussion of the main interfaces and classes of the Java algebra system.

Last modified: Wed Mar 31 22:45:31 CEST 2021