Funktionen höherer Ordnung
In der Mathematik Summe_{i=1,n} f(i) oder auch Produkt_{i=1,n} f(i)
Zum Beispiel die Lisp-Funktion summe:
(define (summe f a b)
(if (> a b)
0
(+ (f a)
(summe f (+ a 1) b)
)
)
)
(define (id x) x)
(define (sqr x) (* x x))
(summe id 1 4)
10
(summe sqr 1 4)
30
Lösung in Java
Mit einem Interface und
public interface SummenFunktion {
public double f(int i);
}
public class Summation {
double summe( SummenFunktion sf, int a, int b ) {
double sum = 0.0;
for (int i = a; i <= b; i++) sum += sf.f(i);
return sum;
}
}
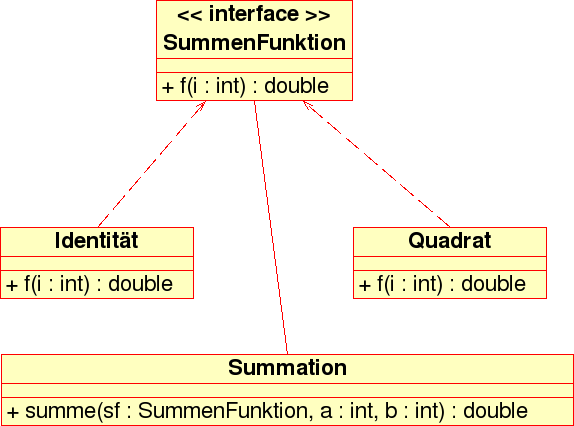
Summation UML Diagramm
public class Identitaet implements SummenFunktion {
public double f(int i) {
return (double) i;
}
}
public class Quadrat implements SummenFunktion {
public double f(int i) {
double d = (double) i;
return d*d;
}
}
public class SummenTest {
public static void main(String[] args) {
Screen out = new Screen();
Summation s = new Summation();
SummenFunktion sf = null;
double sum = 0.0;
sf = new Identitaet();
sum = s.summe( sf, 1, 4);
out.println("Summe von 0 bis ? von f(i) = i ist "
+ sum);
sf = new Quadrat();
sum = s.summe( sf, 1, 4);
out.println("Summe von 0 bis ? von f(i) = i*i ist "
+ sum);
}
}
Zum Beispiel die Lisp-Funktion operation:
(define (operation op init f a b)
(if (> a b)
init
(op (f a)
(operation op init f (+ a 1) b)
)
)
)
(operation + 0 id 1 4)
10
(operation + 0 sqr 1 4)
30
(operation * 1 id 1 4)
24
(operation * 1 sqr 1 4)
576
Lösung in Java
public interface Operation {
public double getInit();
public double operation( double x, double y);
}
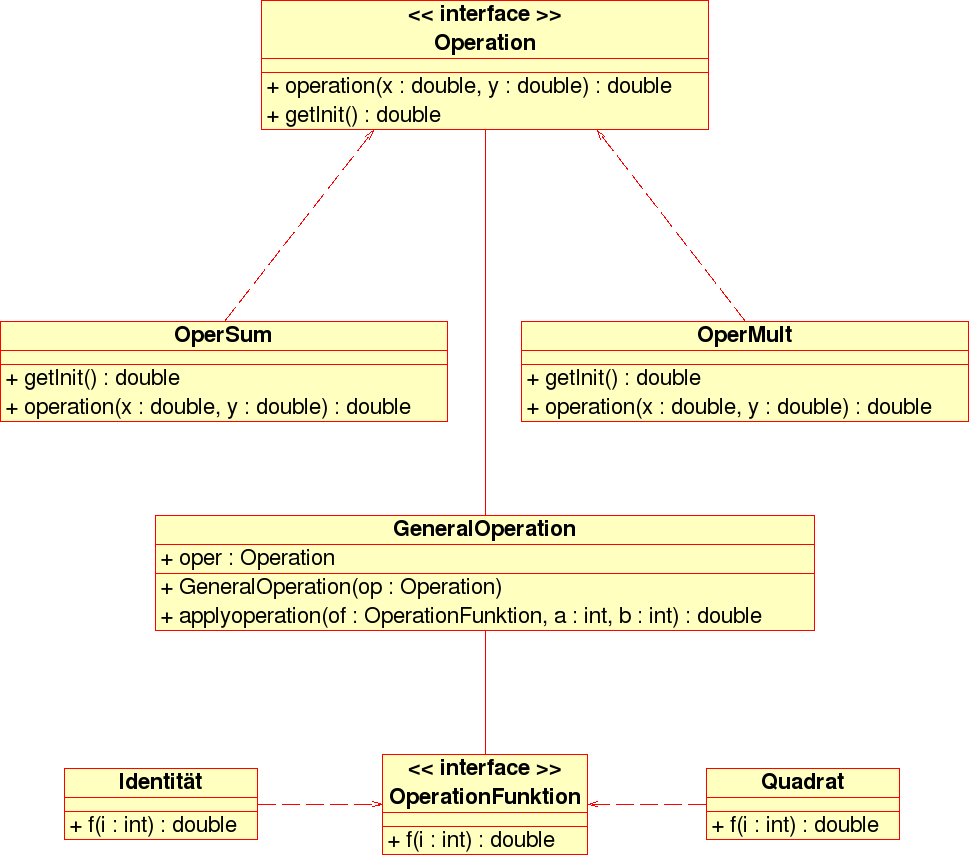
Operation UML Diagramm
public class OperSum implements Operation {
public double getInit() { return 0.0; }
public double operation( double x, double y) {
return x + y;
}
}
public class OperMult implements Operation {
public double getInit() { return 1.0; }
public double operation( double x, double y) {
return x * y;
}
}
public interface OperationFunktion {
public double f(int i);
}
public class GeneralOperation {
Operation oper = null;
public GeneralOperation( Operation op ) {
oper = op;
}
public double applyoperation( OperationFunktion of,
int a, int b ) {
double res = oper.getInit();
for (int i = a; i <= b; i++)
res = oper.operation( res, of.f(i));
return res;
}
}
public class OperationTest {
public static void main(String[] args) {
Screen out = new Screen();
OperationFunktion of = null;
double erg = 0.0;
Operation sum = new OperSum();
GeneralOperation summe = new GeneralOperation( sum );
of = new Identitaet();
erg = summe.applyoperation( of, 1, 4);
out.println("Summe von 0 bis ? von f(i) = i ist "
+ erg);
of = new Quadrat();
erg = summe.applyoperation( of, 1, 4);
out.println("Summe von 0 bis ? von f(i) = i*i ist "
+ erg);
Operation prod = new OperMult();
GeneralOperation product = new GeneralOperation( prod );
of = new Identitaet();
erg = product.applyoperation( of, 1, 4);
out.println("Produkt von 0 bis ? von f(i) = i ist "
+ erg);
of = new Quadrat();
erg = product.applyoperation( of, 1, 4);
out.println("Produkt von 0 bis ? von f(i) = i*i ist "
+ erg);
}
}